Trying to solve a rate of change problem. Similar to one in the database
Find the rate of change of the distance between the origin and a moving
point on the graph of y = x(squared) + 1 if dx/dt = 2 centimeters per
second .
I am sending this for my daughter a senior taking high school calculus. I
have had differential equations and multivariate calculus but I cannot
remember a thing!
Frank
Hi Frank,
I sketched the curve and marked a point P on the curve with first coordinate x. Since the curve is
y = x2 + 1
the point P has coordinates (x, x2 + 1).
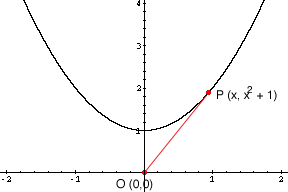
Let s(x) be the distance between the origin O and the point P then
s(x) = [(x2 + (x2 + 1)2 ]1/2 = [x4 + 3 x2 + 1]1/2
x is a function of time t so s(x) is a function of time and you can differentiate s(x) with respect to t.
d/dt (s(x)) = 1/2 [x4 + 3 x2 + 1]-1/2 (4 x3 dx/dt + 6 x2 dx/dt )
Substitute dx/dt = 2 centimeters per second and you have an expression that gives you the rate of change of the distance between the origin and an arbitrary point P on the curve.
Penny