Here is one problem I don’t understand.

Given: ABCD is a quadrilateral; <A is congruent to <C; <B is congruent to <D

Prove: ABCD is a parallelogram

Hi Hanna,

Different books might define a parallelogram differently but I am going to assume that your book defines a parallelogram as "a quadrilateral with both pairs of opposite sides parallel". I am also not sure what facts you know but let me try a proof.

I have reproduced your diagram below with two additional constructed line segments. Extend the line segment DC to a point E and extend the line segment DA to a point F.

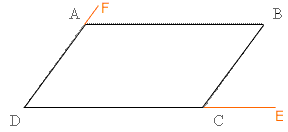
I can conclude that the sides AB abd CD are parallel if I can show that <CBA and <ECB are congruent. You know that the measure of the four interior angles of a quadrilateral add to 360 degrees, thus

measure(<A) + measure(<B) + measure(<C) + measure(<D) = 360 degrees

But angles A and C are congruent and angles D and B are congruent. Hence

measure(<C) + measure(<B) + measure(<A) + measure(<B) = 360 degrees

so

measure(<C) + measure(<B) = 180 degrees ---- equation 1

Also DCE is a straight line so measure(<BCD) + measure(<BCE) = 180 degrees. That is

measure(<C) + measure(<BCE) = 180 degrees ---- equation 2

Hence from equations 1 and 2

measure(<B) = measure(<BCE)

that is

measure(<CBA) = measure(<BCE)

Hence the sides AB and CD are parallel.

Now use the extension of the line segment DA to F to show that the sides AD and CB are parallel.

Penny

Go to Math Central