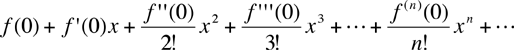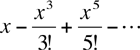Hi Holly,

I can give you examples of a couple of places where the third derivative is used.

In the classic application of calculus to the motion of a point on a line, if s(t) is the position of the point then s'(t) is the velocity and s''(t) is the acceleration. The third derivative would then be the rate of change of acceleration. This is normally called a jerk. There is a note at the University of California Riverside called What is the term used for the third derivative of position? that you might find useful. To quote from this article

"As its name suggests, jerk is important when evaluating the destructive effect of motion on a mechanism or the discomfort caused to passengers in a vehicle."

A second place where the third and higher derivatives are used is in series approximations. Some functions are difficult to evaluate, in particular trigonometric functions and logarithms but for these functions there are approximations that can be used, and these approximations often involve derivatives. For example a sufficiently nice function f(x) (one where the derivatives exist) can be approximated for x close to zero by

where n!= n(n-1)(n-2)...1 and f⁽ⁿ⁾(x) is the n^th derivative of x. Thus, in particular, near zero sin(x) is approximately

For a particular evaluation the number of terms used depends on the accuracy required in the approximation. This series is called a Taylor Series or a Maclaren Series.

When you use your calculator to find the sine of an angle there is a similar approximation used. It is probably not the series above as there are other approximations that are better suited for this, but the mathematics behind the approximations often involve higher order derivatives.

Harley

Go to Math Central