a belt is stretched around two pulleys whose centers are d units apart and whose radii are R and r respectively (obviously R+r<d). the challenge is to find the length of the belt, l as a formula in terms of R, r, and d only.
Hi Ian,
I drew a labeled diagram.
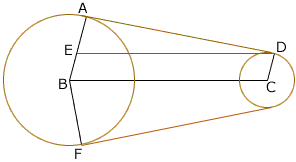
|AB| = |BF| = R, |CD| = r and |BC| = d. The belt section AD is tangent to the large pulley at A so angle DAB is a right angle. The line DE is constructed parallel to CB so |DE| = d.
Since triangle AED is a right triangle
|DE|2 = |EA|2 + |AD|2
that is
d2 = (R - r)2 + |AD|2
Solve for |AD|.
Since ED and BC are parallel angle AED and angle ABC are equal. But angle AED is the inverse tangent of |AD|/|AE| . The measure of angle ABF is twice the measure of angle ABC and hence you can now find the length of the longer of the two arcs joining A and F.
Angle BCD is 180 degrees minus angle ABC and hence you can also find the length of the appropriate arc on the smaller pulley.
Harley