My name is James. I am an (out of practice) transportation technician. I hope I can explain my problem clearly. Imagine a vertical line 1.107' tall. Leaving the top of this line, sloping down to the right at a 4:1, at what horizontal distance will the line strike a second line, which leaves the the bottom of the vertical line sloping down to the right at a rate of .02 ft/ft (or 2%)? There is a fairly easy solution to this, but I have lost my notes!
Can you help?
Hi James,
I imagined a coordinate system with the base of your vertical line at the origin (0,0) and the top at (0,1.107). The line that leaves the bottom of the vertical line and slopes downward at a slope of 0.02 has equation y = -0.02 x
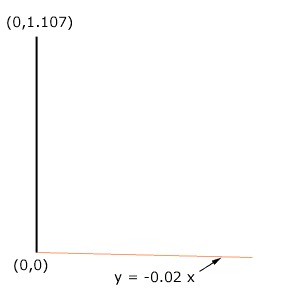
I am not sure what you mean by "sloping down to the right at a 4:1". If you mean that the line drops vertically by 4 feet for every one foot in the horizontal direction then the slope is -0.25 and the equation of the line is y - 1.107 = -4 x.
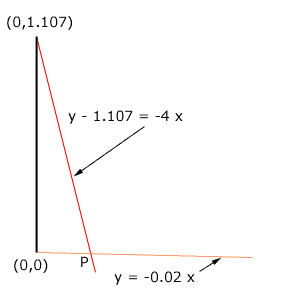
If this is the situation then you can find the horizontal distance between the base of the vertical line and the point P where the lines intersect by solving the two equation for x.
Substitute the y value for the first line, y = -0.02 x, into the second equation to get
-0.02 x - 1.107 = -4 x, or
3.98 x = 1.107
Hence
x = 1.107/3.98 = 0.278 feet.
If by "sloping down to the right at a 4:1" you mean that the line drops vertically by 1 foot for every 4 feet in the horizontal direction then the slope is -0.25 and the equation of the line is y - 1.107 = -0.25 x.
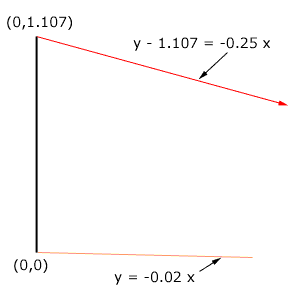
If this describes your situation then solving for x gives
-0.02 x -1.107 = -0.25 x
0.23 x = 1.107
x = 4.81 feet.
Harley