Hi Jessica,

I am not sure what formulas you are using. I don't rremember very many formulas but I can show you how I find surface areas of the figures you describe.

Cylinder

Imagine that your cylinder is a soup can with the top and bottom removed. Suppose the radius of the end is r and the height is h.

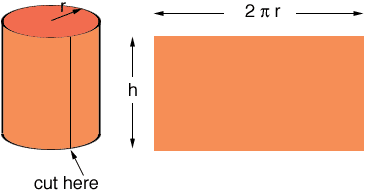
Cut along the line indicated and roll out the can. You now have a rectangle of dimensions 2 r by h and hence an area of

2 r h.

If you want to include the ends of the can in the surface area you need to add

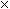
2 r²

Regular Pyramid

Suppose the the sqare base of the pyramid has side length x, then the area of the base is x² The remainder of the surface is three, congruent triangles.

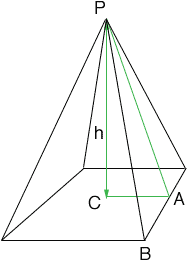
Let P be the apex of the pyramid and A be the midpoint of one of the sides of the base. |PA| is the height of the triangular face and hence you can find the area of this triangle if you can find |PA|.

If you know the height of the pyramid (h in the diagram) then PCA is a right triangle wit sides of length h and ^x/₂. |PA| can then be found using Pythagoras' Theorem.

PBA is also a right triangle so if you know |PB| you can use Pythagoras' Theorem again to find |PA|.

Right Cone

For the surface area of I right cone look at Walter's answer to an earlier question.

Prism

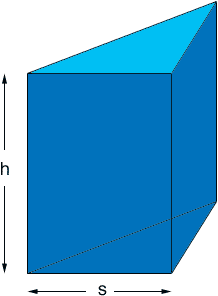
The diagram I drew is for a right, triangular prism but the idea is the same regardless of the shape of the polygon that forms the base.

The surface area is

2 (the area of the base) + (the sum of the areas of the sides)

In a right prism the sides are rectangles so each side has area

(length of a side of the base) (height)

If the prism is not a right prism then the sides are parallelograms and you then need to use whatever facts you know about the prism to find the dimensions of the parallelograms.

Penny

Go to Math Central