I am a builder working on a project where I need to make a cone. It's a right circular cone with 15" base radius and slant angle of 30 degrees. I want to cut it out of flat sheet metal then bring the edges together to form the cone. Is this enough information? How do I figure this out?
Thank you,
John
Hi John,
There are some diagrams and an explanation of the calculations in Harley's answer to an earlier question from Steve. I have reproduced the diagrams below.
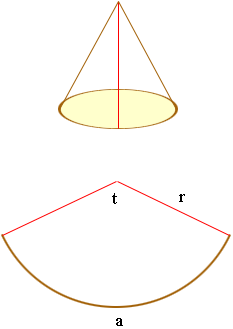
Harley then points out that a = r ![]() t
where t is the angle measured in radians. From the situation you describe,
in the diagram below you know that the length of AB is 15 inches and
the angle ABP is 30 degrees.
t
where t is the angle measured in radians. From the situation you describe,
in the diagram below you know that the length of AB is 15 inches and
the angle ABP is 30 degrees.
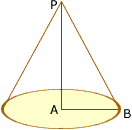
The fact that angle ABP is 30 degrees and that the angle PAB is a right angle tells me that the length of BP is twice the length of AB so the length BP is 30 inches. That is the r in Harley's diagram.
Also the length of the arc a is the circumference of the circle that forms the base of the cone so
a = 2
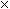
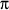
15 = 30
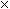
inches.
Thus, since a = r ![]() t
,
t
,
30
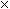
= 30
t, or
t =radians.
But ![]() radians is
180 degrees so if you draw a semicircle of radius 30 inches and roll
it up you will get the cone you describe.
radians is
180 degrees so if you draw a semicircle of radius 30 inches and roll
it up you will get the cone you describe.
Penny