Quandaries
and Queries
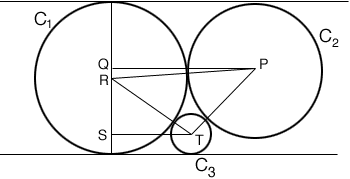
Two circles, C1 and C2, touch each other externally; and the line l is a common tangent. The line m is parallel to l and touches the two circls C1 and C3. The three circles are mutually tangent. If the radius of C2 is 9 and if the radius of C3 is 4, what is the radius of C1?
Hi Kate,
I drew a diagram and labeled some points. P, R and T are the centers of the circles. PQ and ST are parallel to the common tangent lines m and l.
I then redrew part of the diagram, larger so that I can include some dimensions. I let r be the radius of C1.
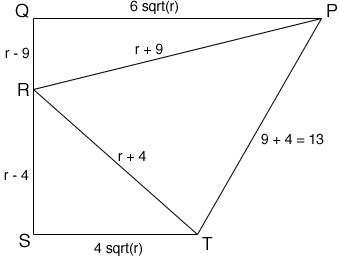
Since PQ and ST are parallel to the tangent lines. PQR and RST are right triangles and hence Pythagoras' Theorem can be used to find the lengths of PQ ans ST. Now draw a line trough T, parallel to SQ and meeting PQ at W.
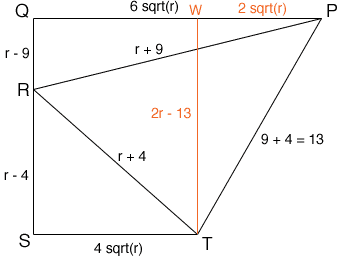
PWT is a right triangle and hence Pythagoras' Theorem applied to this triangle gives a quadratic you can solve for r.
This is one configuration for the circles you describe in your problem but there is at least one other configuration.
Chris