Hi Martha,

Since this is an isosceles triangle you can find the height using Pythagoras Theorem. First find the midpoint M of the 60' base and then join this point to the vertex A of the triangle as in the diagram below.

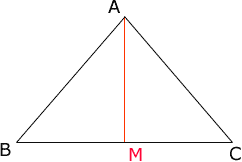
Since |AB| = |CA| , |BM| = |MC|, and |AM| = |AM|, the triangles ABM and AMC are congruent. Hence angles BMA and AMC are equal. Since there sum is 180^o each is 90^o and thus triangle ABM is a right triangle. Hence Pythagoras Theorem tells us that

|AB|² = |BM|² + |MA|²

that is

37² = 30 ² + |MA|²

and hence the height |MA| of the triangle is

|MA| = Sqrt(37² - 30²) = 21,66 square feet.

The fact that the triangle is isosceles was needed here to show that triangle ABM is a right triangle. An alternate procedure to finding the area is to use Heron's Formula.

Penny

Go to Math Central