My Name is Mike and I teach high school. I had a student ask me to explain why .9 repeating is equal to 1. Then he asked me about an asymptote, or why a parabola or any other curve for that matter can continually approach a value (like 1) and yet never attain a value of 1. He is thinking that these two should represent the same concept and yet they contradict each other. Do you have a solid explanation for him? Of by the way he is a 7th grader. Great little thinker!!!!!
We have two responses for you. One from Claude and another from Harley.
Hi Mike,
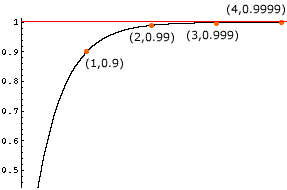
You can graph a curve going through the points
(1, 0.9), (2, 0.99), (3, 0.999), (4, 0.9999), ...
The asymptote is the line y = 1, and the fact that the curve never touches the asymptote means that none of the finite decimals 0.9, 0.99, 0.999, ... is really equal to 1.
Another problem for great little thinkers: Start with a full pizza, eat half of it on the first day, half of what is left on the second day, half of what is left on the third day, and so on: every day you eat half of what is left. How does it end?
Claude
Hi Mike,
I don't think that the two concepts contradict each other, but they certainly are different. They are two kinds of infinity, Aristotle called them potential infinity and actual infinity. Potential infinity is is seen in an ongoing process or motion without end. You see that when you imagine building a series of regular polygon with more and more sides. Actual infinity is infinity conceptualized as a realized "thing". An example is the collection of positive integers which is the "end result" of constructing them as 1,2,3,... Not the repetitive process of adding 1 to the previous number but the end result, the infinite set of positive integers.
Both of your processes, a curve that continuously approaches a value (asymptote) and the process of continually appending another 9 to the decimal representation (0.9, 0.99, 0.999,...) are examples of potential infinity; ongoing processes without end. For the second process however there is an end result or thing, it is the number 1.
Much of what I have said here comes from George Lakoff and Rafael E. Nunez, Where Mathematics Comes From, Basic Books, New York, 2000. pp 158. This book is much too advanced for your great little thinker but some of the ideas and conundrums are not. He came up with one himself.
Harley