Question:
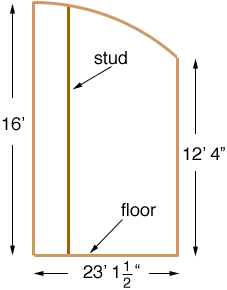
I'm framing a building wall with a curved (arcing) top section. The radius of the section is 74'6" with a height above finish floor of 16'0". The horizontal run of the arced section is 23' 1 1/2" with a low height above finish floor of 12'4". If I start with a 16' stud at the high end how long are the subsequent studs if they are on 16" centers? Short of laying this out on a tennis court how can I work out the lengths of the studs?
Hi Mike
I drew a diagram of what I understand to be your situation with 1 stud in place. (The horizontal scale is incorrect. I see why you need a tennis court.)
I changed all the units to inches and drew a section of the large circle with radius 74'6" (894") showing where I see the building wall fitting into the circle. The height of the floor above the center of the circle is 74'6" minus 16' or 702". The horizontal run is 277.5".
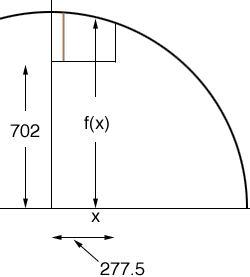
The equation of the top half of a circle of radius r is
f(x) = Sqrt[r2 - x2]
or in your case
f(x) = Sqrt[799236 - x2]
The studs are at x = 0", x = 16", x = 32",... and hence the lengths of the studs in inches are
f(0) - 702, f(16) - 702, f(32) - 702,...
I did these calculations and got
192., 191.857, 191.427, 190.71, 189.706, 188.413, 186.831, 184.957, 182.789, 180.326, 177.566, 174.504, 171.139, 167.467, 163.483, 159.183, 154.563, 149.617
As a check that these numbers look correct we know the final stud is only 5.5" from the 149.617" stud and its length is 12'4" or 148" so my numbers look reasonable.
Penny