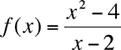Hi,
My name is Nicole and I am a teacher at Weyburn Comprehensive School. I am currently teaching both Math B30 and Calculus 30 at the school and I have a question about rational functions. I know that if a rational function (by definition) has common factors in the numerator and the denominator then it is not a rational function (math b30) however in calculus this common factor creates a hole in our graph. Can you explain to me why a common factor or constant does not give us a rational function?
I hope you understand what I am trying to ask! Thanks!
Nicole
Hi Nicole,
I think the confusion here arises from the fact that we are sometimes sloppy when we talk about functions. The sloppiness is that we write an expression for a function that describes how the function behaves, but we don't explicitly describe the domain of the function. We let the form of the function determine the domain. For example let
and
We usually simplify f(x) and write
We then conclude that f(x) = g(x) but, in fact, this conclusion is incorrect. f(x) and g(x) are different functions since their domains are different. The domain of g(x) is all real numbers and the domain of f(x) is all real numbers except x = 2. The cancellation to get the last equality above is only valid if x is not 2. If x is 2 then the denominator is zero and we can't cancel it. The functions "behave the same" for all x where they both exist, but f(x) does not exist if x is 2.
Also you say "if a rational function (by definition) has common factors in the numerator and the denominator then it is not a rational function". I prefer a definition that is inclusive. I would say that
a rational number is a number that can be written a/b where a and b are integers, b not zero.
This means, for example that 5 is a rational number since 5 can be written 5/1.
Likewise I would say that
a rational function is a function that can be written p(x)/q(x) where p(x) and q(x) are polynomials.
So, as above this means that g(x) = x + 2 is a rational function since it can be written
g(x) = (x - 2)/1 , but it is not The rational function f(x) since they have different domains.
Penny
Hi Nicole,
Section 4.4 of B. Thiessen's Math B30 text states, "For the purposes of our discussion we will define a rational function as a function that is formed by taking the ratio of two polynomial functions that have no common factor other than plus or minus 1."
I believe that our Saskatchewan Math B30 course focuses on those rational functions that have no common factors in the numerator and denominator but this does not mean that a rational function with common factors isn't a rational function....the course simply has chosen to not use these kind of rational functions for the purposes of meeting the curriculum objectives. Perhaps this is to avoid over-complicating the graphing procedure so students can focus on those graphs with asymptotic behaviour rather than those whose graphs have "holes" but would otherwise be continuous polynomial graphs.
I hope this makes sense!
Leeanne