Quandaries and Queries
  

 

Does anyone have a formula for calculating the chord length for a segment of a circle when you know the radius and the enclosed angle or radian ?

Thanks in advance .
 

 

Hi,

I drew a circle of radius r and center C, and a chord AB. The point M is the midpoint of the chord AB.

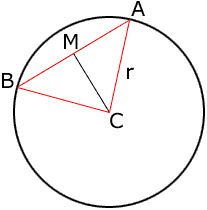
M is the midpoint of AB so

|AM| = |BM|

MC is common to both triangles AMC and MBC and

|AC| = |BC| = r.

Thus triangles AMC and MBC are congruent. Hence angles AMC and BMC are comgruent and their sum is 180o. Thus the measure of angle AMC is 90o.

Thus, since triangle AMC is a right triangle,

|AM|/|AC| is the sine of the angle MCA.

But angle BCA is twice angle MCA, and hence

|AB| = 2 |AM| = 2 |AC| sin( BCA/2)

Penny

 
 

Go to Math Central