Hi, my name is Regis.
I am a student.
The level of the question is secondary (11).
The question is:
The average monthly temperature for a location in Ontario as a function
of month number can be modelled using the equation y = a cos[k(t +
b)] + d. If the highest average monthly temperature is 20 degrees C
and the lowest average monthly temperature is -10 degrees C, which
occurs in January (month 0) with an annually repeating pattern, write
the simplest equation that models this relationship and use the equation
to calculate the average temperature in September.
Hi Regis,
I really like this problem. I am going to get you started the way I think about this problem and you can continue. If you have problems completing it let me know. (I may have changed your notation slightly.)
When I see the instructions to model using a cosine function then, in my mind I see
y = cos(t)
The shape of this function is what you need but the axes are in the wrong place and the scales on both axes need to be changed.
Your model calls for a repeated pattern starting with the cosine at its minimum (-10 degrees C in January), thus the y-axis need to go through the minimum value of the cosine function. You can accomplish this by adding 180o to the x-values. (From now on I will only plot one cycle of the cosine function.)
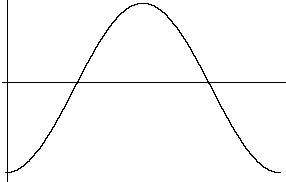
y = cos (t + 180o)
The scale on the y axis needs adjustment. In the graph above the values of the function are from -1 to 1, a range of 2 units. Your function is to have values from -10 degrees C to 20 degrees C, a range of 30 units. Thus I need to multiply the cosine function by 30/2 = 15. This gives values of the funtion from -15 to 15 and you want -10 to 20, so add 5 to the y-values.
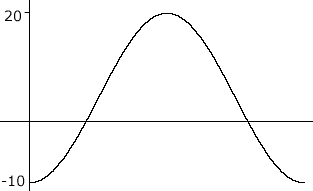
y = 15 cos(t + 180o) + 5
All that remains is the scale on the x-axis. At the moment the one cycle shown on the graph above is for t from 0o to 360o. You need the scale on the x-axis to be in months so that one cycle is from month 0 (January) to month 12 (which is January again).
Harley