Want to make an elliptical table, say the long (major) axis is 4 feet, and the short (minor) axis is 3 feet.
I can construct this figure, but I'm trying to figure out what the exact dimension of a rectangle within this ellipse will be if I make the table a drop leaf type where the drop dimensions are equal for each end of both the long and short axes. Intuitively, it looks like there is one and only one solution.
Regards,

Phil's table
Hi Roger,
Your ellipse has semi-axes of length 2 and 3/2 so it has equation
x2/4 + 4 y2/9 = 1
I let z feet be the width of the drop leaf and (p,q) be a point on the ellipse which will be a corner of the rectangular table, as in the diagram.
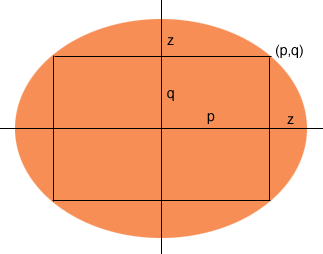
Since the lengths of the minor axes are 2 and 3/2 ,
p + z = 2 and q + z = 3/2
Hence
p = 2 - z and q = 3/2 - z
Since (p,q) is on the ellipse the coordinates must satisfy the equation of the ellipse, so
p2/4 + 4 q2/9 = 1
I substituted p = 2 - z and q = 3/2 - z and simplified to get the quadratic
25 z2 - 84 z + 36 = 0
Solving this with the general quadratic gave me
z = (84 + 58.7877)/50 or z = (84 - 58.7877)/50
that is
z = 2.86 feet or z = 0.5042 feet.
Clearly the first solution is irrelevant to your problem so the width of the drop leaf is 0.5042 feet or 6.05 inches.
I was quite surprised that the width is so close to 6 inches, the difference is less than the width of your saw blade.
Penny
Note: Two and a half months after sending us this question Roger wrote back to say that his friend Phil had built the table. He included the photograph at the top of this page.