I am currently researching a patch disease of grasses. These patches are roughly circular. I need a term for a line from the center of the patch to the periphery. Since the patches are not perfectly circular, my supervisors tell me I cannot use the word 'radius'. What else could I use?
Hi Sandrine,
I have a few suggestions for you. One comes from Denis.
In graphs we talk about the center as a point(s) of minimum eccentricity (min max distance to other points). So if no word exists as requested they could use eccentricity.
I am not sure that Denis has the correct parameter in mind. I have a couple of suggestions but I am also not sure I am thinking of the correct parameter.
We use the term radius of a circle for two different concepts. One is a line segment from the center of the circle to the periphery, and the other is the length of this line segment.
If the former is the concept you have in mind, as you say in your question, then I might use the term "a ray" or "a central ray". To me the word ray carries a connotation of direction and I don't know if this is important to you.

If you are looking for a name for the length of this "ray" then another concept comes to mind.
The "width" of a closed convex curve is defined as the distance between parallel lines bounding it ("supporting lines").[1]
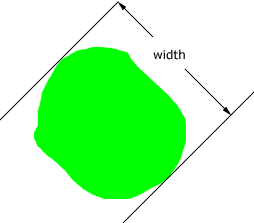
The width of a curve is usually different in different directions. For a circle the width and diameter are the same, and the radius is half the diameter. If this is the meaning of "radius" you are trying to abstract you might call it "a half-width".
I hope this helps.
Harley
An another response from Walter.
This is an interesting question.
It appears there is a designated 'center' for the patch. Once we have that, one can have 'radial segments' out from the center to each of the points on the edge. This is probably a good term to use - connects with what mathematicians would say, if we were using 'polar coordinates'.
There is another term which geometers use for these types of shape: diameter.
If you squeeze the shape between two parallel lines on either side, you can measure the distance between the lines. This is a 'diameter'. You can try all all possible directions and find out what the largest and smallest diameter are - or perhaps find something with all diameters the same (but still not a circle). Perhaps this is of some use to you.
(What Walter calls diameter I called width. Harley)