Quandaries
and Queries
Hello,
My name is Sherry and I am a student. My question is regarding secondary level geometry proofs. I am having much difficulties with the following proofs. I have to answer one as a paragraph proof, one as a flow chart proof and two as a two-column proof. The proofs are as follows:
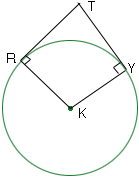
1. If Circle K has tangents RT and TY where R and Y are the points of tangency, then angle RKY and angle RTY are supplementary.
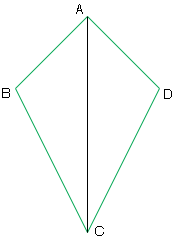
2. If one diagonal bisects a pair of opposite angles in a quadrilateral, then the quadrilateral is a kite.
3. Write an analytical proof:
Given: Triangle OBC with midpoints D, E, and F of OC, OB, and BC respectively.
Prove: Area of triangle FDE = 1/4 Area triangle OBC
4. Write an indirect proof to show that the measure of an exterior angle of a triangle is equal to the sum of the two remote interior angles of the same triangle.
These are the four proofs that I need help understanding. Any help would be greatly appreciated.
Hi Sherry,
I am not going to do your homework but I will give you some hints.
-
K is the center of the circle. Since RT is tangent to the circle at R, the angle KRT is a right angle. Likewise KYT is a right angle.
- I called the quadrilateral ABCD. Angles DAC and CAB are congruent and angles DCA and ACB are congruent. Show triangles ACD abd ABC are congruent.
Penny