Hello,
My name is Stan. I am just a regular guy (high school grad back in the early 1960s). I guess that my question would be at the middle or high school level. Here's my question: I own a parcel of land (lot 20) that is assessed at 9127.00 square feet and has a frontage of 99.90 feet according to the tax roll. I don't know how large my property actually is since I feel that the tax assessment and the survey map don't jive. The property is a trapezoidal shaped piece of land with a curve at the front. On the north side it is 50.932m long and on the south side it is 34.927m. The west side is 20.122m long and the east side is the curve with a radius of 18.300m. The north side and the west side meet at a 95 degree angle and the south side and the west side meet at an 85 degree angle. Just how big is my land? I have attached a pdf of the survey map and included the map above. Can you be of some assistance?
Thanks,
Stan
Hi Stan,
Below I reproduced part of the survey map you sent abd marked the four corners of the lot. I also drew a line A, perpendicular to the to the south side B D and meeting that side at C.
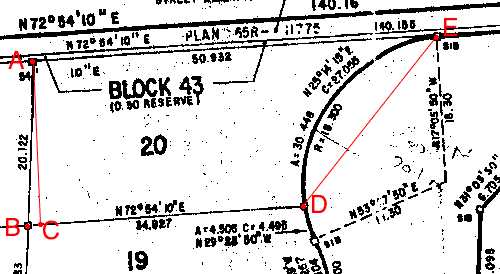
ABDE is a trapezoid with AE and BD parallel so the area of the trapezoid is
(|AE| + |BD|)/2
|AC|.
Angle ABC is 85o so |AC| = |AB| sin(85o)
= 20.122 0.9962 = 20.045m.
Hence the area of the trapezoid is
(50.932 + 34.927)/2
What remains is to subtract the area of the bite taken out of the trapezoid by the circular arc. For this I redrew the diagram with coordinates in meters, putting B at the origin and the south side along the X-axis. P is the center of the arc through D and E and Q is the midpoint of the line segment DE.
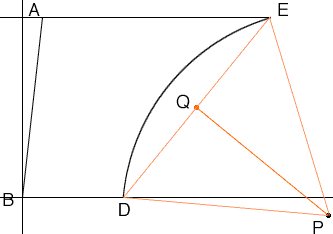
The coordinates of D are (34.927,0), and
the coordinates of A are
(20.122 cos(85o),
20.045) = (1.754, 20.045). Since |AE| = 50.932, the coordinates of
E are (50.932 + 1.754, 20.245) = (52.686, 20.245). Hence Q, as the midpoint
of DE has coordinates
((34.927 + 52.686)/2, (0 + 20.045)/2) = (43.806, 10.023)
Thus |EQ| = Sqrt[(52.686-43.806)2 + (20.045-10.123)2] = 13.390. Hence, using Pythagoras' Theorem,
|PQ| = Sqrt[18.3002 - 13.3902] = 12.474
Let theta be the angle DPE then
angle QPE = theta/2 = tan-1(|EQ|/|QP|) = 47.029 o = 0.8208 radians.
Hence the area of the sector EDP is
1/2 r2 theta = 1/2 18.32
and the area of the triangle EDP is
1/2
Hence the area of your lot is
860.522 - ( 274.878 - 167.027) = 752.671 m2
There are 3.28 feet in a meter so the area of your lot is
752.671
I am not sure where the discrepancy is. My area of the trapezoid is 860.522 m2 ( 9257.84 square feet) which is reasonably close to the 9127.00 square feet that you have for the lot.
On the map, along the arc is the figure A = 30.448 which I assume is the length of the arc. 30.448 meters is 99.9 feet so that is your frontage measurement. That is not what I get for the length of the arc ED. Perhaps it is not actually an arc of a circle.
Harley