im trying to make a 6 sided (hexagon) pyramid, from 6 triangles of 12mm plywood, i know all the angles to cut apart from the one one to join all 6 triangles together. Rough measurements are outer edge (A) of each triangle is 13cm's, length of other 2 sides (B&C) of triangle outside to center is 14cm's with a height of the whole thing together about 6cm's. If the hexagon was flat then i wouldn't need to cut an angle but by adding a height i need to cut another angle so the sides are flush. What's the calculation to work this angle out. From what i can figure depending on the height and side lengths of the triangle this angle will differ so just use the measurements above as a guide.
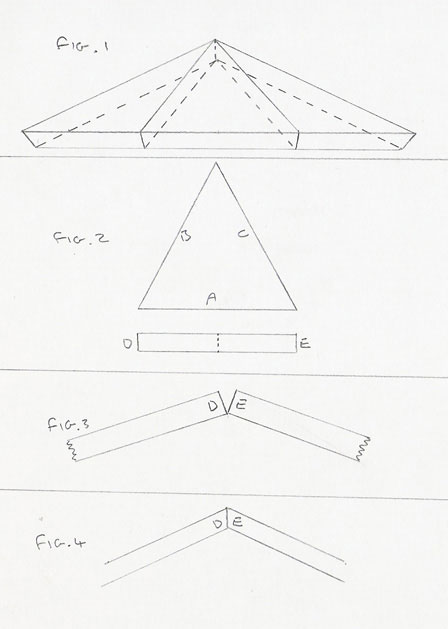
I have included a drawing to help explain the problem. Once the triangle is cut out and looked down upon side A is 13cm B&C 14cm. For all 6 triangles to join flush together there needs to be an angle cut on D&E, this is the angle i can't figure out properly. Fig.1 is the finished product. Fig.2 single triangle. Fig.3 two triangles joined together not cut. Fig.4 two triangles joined with angle cut on either side.
Hi Steve,
This is a nice project. We would like to see it when it is finished.
We are going to use vectors to find the angle you need. The line diagram below shows two of the triangles, PQR and PRS, and the circle with center at the center of the hexagon and radius 13. This circle passes through the six vertices of the hexagon. The height of the pyramid has been extended to reduce the clutter on the diagram.
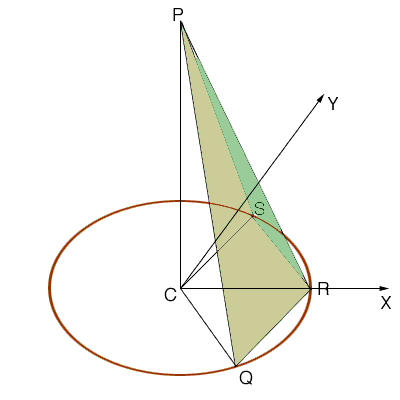
We have overlaid a coordinate system with the origin at the center C of the hexagon, the X and Y as shown and the Z axis vetrical through P. The cordorinates of the labeled points are then
C = (0, 0, 0)
R = (13, 0, 0)
Q = ( 13/2, -13 sqrt(3)/2, 0)
S = ( 13/2, 13 sqrt(3)/2, 0)
P = (0, 0, sqrt(27))
Let u be the vector from CQ, v be the vector from CR, w be the vector CS and t be the vector CP. With this notation
v - u = QR
w - v = RS
t - u = QP
t - v = RP and
t - w = SP
Vectors n1 and n2, perpendicular to the triangles PQR and PRS respectively can be found using the cross product.
n1 = (v - u)
(t - u) = ( 117/2, -39 sqrt(3)/2, 169 sqrt(3)/2)
n2 = (w - v)(t - v) = ( 117/2, 39 sqrt(3)/2, 169 sqrt(3)/2)
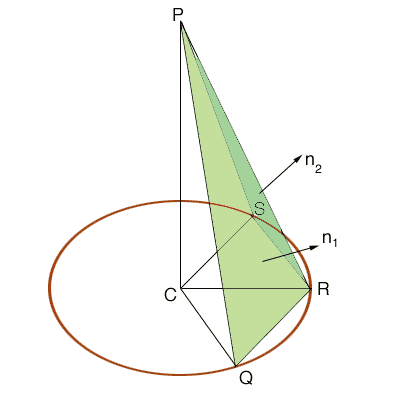
The dot product of the vectors n1 and n2 is given by
n . n2 = |n1| |n2| cos(theta)
where theta is the angle between n1 and n2 and hence
cos(theta) = n1. n2/|n1||n2| = 187/205
Thus
theta = cos-1( 187/205) = 24.19 degrees
The angle between the planes containing the triangles PQR and PRS is then
180 - 24.19 = 155.81 degrees.
Thus, using your Fig. 4
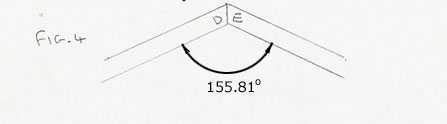
Thus the bevel angle is 155.81/2 = 77.9 degrees.
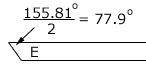
Chris and Harley