Hi,
I'm a middle school grade 7 math teacher. I'm studying for the Massachusetts Teacher's exam and I need some help with tangent lines to circles. If you can take me through the steps for the following problem, I should be able to do the rest. I believe the level would be secondary to college. The problem is:
Your given the equation to a circle (x-3)2 + (y-3)2 = 4 and you need to do 3 things:
1. Find a point on the circle
2. Construct an equation for a tangent line to the circle and through the point
3. Plot the circle, point and the tangent line on one graph
Thanks so much,
Sue
Hi Sue,
Some mathematical expressions are worth recognizing, and the equation of a circle is one of them. A circle with center (a,b) and radius r has equation
(x - a)2 + (y - b)2 = r2
Your circle has equation
(x - 3)2 + (y - 3)2 = 22
and hence a = b = 3 and r = 2. Thus your circle has (center (3,3) and radius 2.Hence I started with part 3 of your question and a plot of the circle.
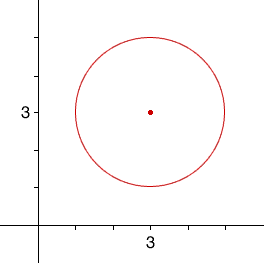
From the graph I can see that the highest point and lowest point on the circle are at x = 3. In the equation, when x = 3 you get
(3 - 3)2 + (y - 3)2 = 22 , or
(y - 3)2 = 22
Thus y - 3 = 2 or y - 3 = -2 and hence the two points on the circle when x = 3 are (3,5) and (3,1). You can chose either one to answer part 1. I am going to chose (3,5).
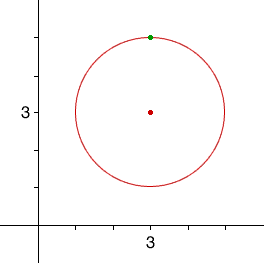
From the diagram the tangent line is the horizontal line through (3,5) and hence the diagram below is an answer to part 3.
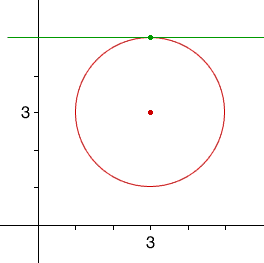
All that remains is to write an equation of the tangent line. I expect that you normally use the equation y = mx + b for the equation of a line. This line os horizontal so its slope is zero (m=0), and it intersects the y-axis at three (b=3), and hence the equation of the tangent line is
y = b.
Penny