We are starting up a new business and for the business we will be required to order concrete for various shapes. Right now we have a job that requires a concrete slab that a decagon it is 140-3/4" from flat side to flat side, 74" from point to center and each flat side is 46" The pad should be 4" thick with 12"x12" continuous footing. I remember learning some of this stuff in college algebra however I have been out of school more years then I am willing to admit. I thank you in advance for your help and look forward to hearing from you soon.

Tanya

Hi Tanya,

I will calculate the volume of the slab you describe and then show you a way to estimate the volume that is easier and probably "good enough". Below is a diagram of a decagon. When you draw the diagonals you can see that it can be divided into ten isosceles triangles.

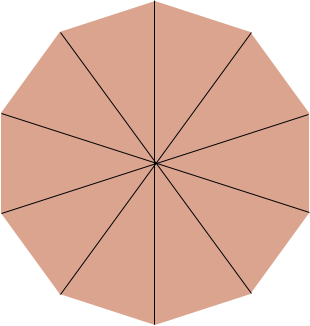
Each triangle has base 46 inches and side length of 74 inches. I drew one such triangle below.

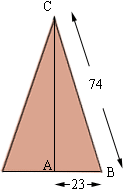
Pythagora's Theorem applied to the triangle ABC gives |AC| = Sqrt[74² - 23² ] = 70.33 inches. Thus the area of each of the ten triangles that make up the decagon is

 ¹/₂ base height = ¹/₂ 46 70.33 = 1617.70 square inches.

Thus the volume of the concrete slab is

10 1617.70 4 = 64708 cubic inches.

One yard is 36 inches so the volume, in cubic yards is

 ⁶⁴⁷⁰⁸/_{(36 36 36)} = 1.39 cubic yards.

My suggestion for an estimation of this volume is to imagine that the concrete slab is a circle of radius 74 inches and thickness 4 inches.

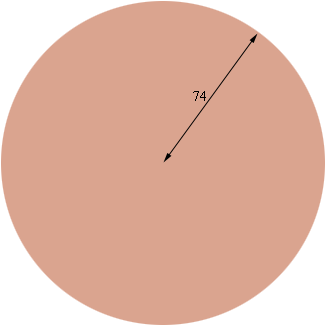
The volume of this slab is

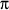
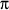
r² thickness = 74² 4 = 68813.44 cubic inches

which is

 ^68813.44/_{(36 36 36)} = 1.47 cubic yards.

The difference between 1.39 and 1.47 cubic yards is quite small and the second calculation is much easier, so I would suggest that for other slabs you use the circle approximation.

By "with 12"x12" continuous footing" I assume you are describing a footing around the perimeter that is 12 inches wide and 12 inches deep. Again I am going to approximate by a circular slab.

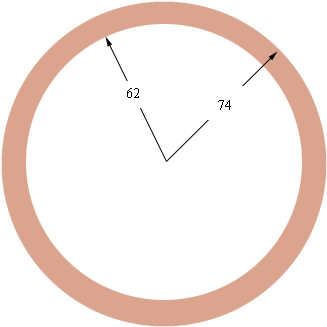
The area of the top of the footing is the area of the outside circle minus the area of the inside circle. That is

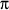
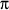
74² - 62² square inches

and hence the volume is

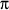
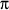
( 74² - 62² ) 12 = 61524.95 cubic inches

or

 ^61524.95/_{(36 36 36)} = 1.32 cubic yards.

It is my experience that the smallest amount of concrete you can order is half a cubic yard so you will need one and a half cubic yards for the footing and then another one and a half yards for the pad.

Harley

Go to Math Central