1.use the heron's formula to find area of triangle ABC to nerest tenth
A.a=21 b=28 c=11
B.a=23 b=28 c=12
2.Find the nearest tenth the altitude of the longest side if a=3 b=3 c=5
3.the length of each side of a rhombus is 10 cm the length of one diagonal is 12 cm find the area to the nearest square centermeter
Hi,
You can find Heron's formula in the answer to a pervious question.
I can see two ways to solve the second problem.
Since a = b = 3 you have an iscosceles triangle and hence, as in the diagram below, if D is the midpoint of the longest side then CDB is a right triangle.
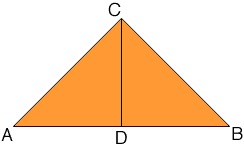
You know the length of BC is 3 and the length of DB is 2 1/2 and hence you can use Pythagoras' Theorem to find the length of CD, which is the altitude you want to find.
The second solution uses Heron's formula.
Use Heron's formula to find the area of the triangle. Call this number T.
From the diagram above the area of the triangle can also be written using the expression that
area = 1/2 base
height
Thus
T = 1/2 base
height
But you know T and the base is 5 so you can solve for the height, which is the length of CD.
For 3 draw a diagram. You will see that the diagonal cuts the rhombus into two congruent triangles. You can again use Heron's formula to find the area of the triangle.
Penny