Please help me with confirming the area in square footage of the irregular pentagon
My Name is Tony and I am working on understanding the square footage as calculated in the drawing. I also believe this is a secondary level question.
I saw the example mathcentral.uregina.ca/QQ/database/QQ.09.03/dana2.html and would appreciate how you worked through the problem, but couldn't find the calculations so that I could adapt them to my sizes.
Your assistance would be greatly appreciated
Thanks you
Hi Tony,
In the example you quote we were unable to work through the problem since there was not enough information given to determine the area. I have the same difficulty with the problem you sent. Below is one of your drawings.
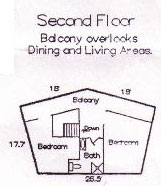
The drawing includes the lengths of the sides of the pentagon but not the size of any of the angles.
I traced your drawing in black and then, to the same scale drew, an orange pentagon with the identical side lengths as are in your drawing. You can see from the drawing that the area inside the orange pentagon is considerably smaller than the area inside the black pentagon.
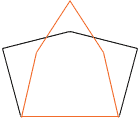
To calculate the area I need the size of one of the angles.
Penny
Hi
Thank you for your quick response and I did more research and have received more information to solve the problem.
This floor plan is from what is referred to as the "14 degree custom floor plan" so I am almost certain the 18' length meet at 14 degrees. I am assuming that the 17.5 walls on the first floor would also meet at 14 degrees.
I only wish I had paid better attention in Geometry and I could be confident in my calculations. I guess I am asking if the calculations that are on the first page appear accurate? I could not follow where some of the dimension came from.
Again thank you in advance for your help and cooperation
Tony
Hi Tony,
I also don't follow where some of the dimensions come from that appear in the table you sent. I want to stick to the second floor since that is the drawing I copied above. I drew it again to a larger scale. I did some rough measurements of angles and the only angle that I can see which might be 14 degrees is the angle PQR in the diagram below.
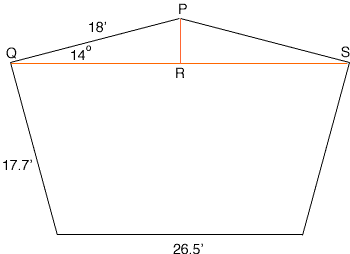
Assuming this angle is 14 degrees,
sin(14o) = |PR|/18 , so
|PR| = 18
sin(14o) = 18
0.2419 = 4.3546 feet
Using Pythagoras' Theorem with the right triangle PQR,
|QR| = sqrt(182 - 4.35462) = 17.4653 feet.
Thus the area of the triangle PQR is
(half the base)
height = 17.4653
4.3546 = 76.05 square feet.
Removing this triangle from the floor plan we are left with the trapezoid in the diagram below.
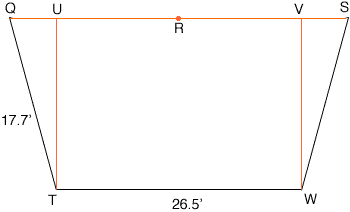
Since |QS| = 2 ![]() |QR|,
and |QV| = (|QS| - 26.5)/2,
|QR|,
and |QV| = (|QS| - 26.5)/2,
|QU| = 4.2153 feet
Again using Pythagoras' Theorem, this time for the right triangle UQT,
|UT| = sqrt(|QT|2 - |UQ|2) = 17.1907 feet.
Hence the area of the rectangle VUTW is
26.5
17.1907 = 455.55 square feet.
Finally the area of the triangle UQT, which is the same as the area of the triangle SVW, is
(half the base)
height = 4.2153/2
17.1907 = 36.23 square feet.
Hence the area of the second floor is
76.05 + 455.55 + 36.23 + 36.23 = 304.06 square feet.
The table you included gave this area as 605.69 square feet so we differ by less that 2 square feet. I think that this is well within round off error, depending on exactly how the calculations were done.
Penny