Quandaries and Queries
  

 

Hi I'm a grade 8 math teacher.
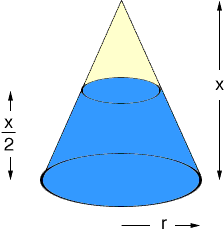
There are 2 right cones, height is X. one of them is filled from the
bottom up (round side) = x/2, when you invert the cone and add the same
amount of liquid inside the second cone, what is the HEIGHT of the liquid?
(thin side)
you need 2 diagrams.
 

 

Hi Vasuki,

I drew a diagram of the cone filled to half the height and I labeled the radius of the base circle r.

The volume of a cone is

 1/3 (radius of the base)2 height

so the volume of this cone is

 1/3 r 2 x

I am going to find the volume of liquid in the cone by subtracting the volume of the unfilled part of the cone. To do this I need to find the radius of the base of the unfilled part of the cone. This involves a use of similar triangles.

In the diagram below triangles ABC and ADE are similar and hence

 |AB|/|BC| = |AD|/|DE| or

 x/r = (x/2)/|DE|

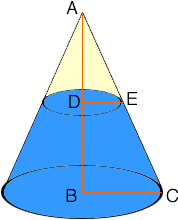
Thus |DE| = r/2

Thus the volume of liquid in the cone is

 1/3 r 2 x -  1/3  (r/2)2 x =  1/4 r 2 x

Now turn the cone over.

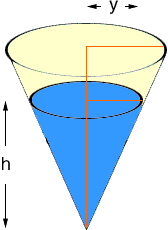
Now I have labeled the height of the liquid h and the radius of the circle at the top of the liquid y. Thus the volume of the liquid is

 1/3 y 2 h

But the volume of the liquid hasn't changed so

 1/3 y 2 h =  1/4 r 2 x

Again using similar triangles, this time from the diagram above

 y/h = r/x

so

y = (r h)/x

Substitute this value of y into

 1/3 y 2 h =  1/4 r 2 x

and solve for h. I got the cube root of 3/4, times x.

Penny

 
 

Go to Math Central