Quandaries
and Queries
AFB
secondary (10-12)
student
Hello, I received a question on my test and I did not know how to approach the question. My teacher would like us to re-do the questions that we got wrong. Here's the one that I need help in:
City A is 30 miles directly north of City C, and City B is 40 miles directly east of City C. Cities A and B are connected by a straight road. Find the length of the shortest path from City C to the road that connects A and B.
Hint: The shortest path, segment CD, is the length of the perpendicular from C to segment AB. First, find AB, AD, and BD.
I would really appreciate if you will be able to take out the time to help me. Thank you in advance!
Hi,
Did you draw a diagram?
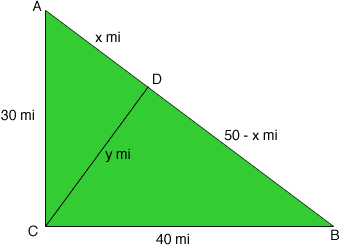
Since triangle ACB is a right triangle, you can use Pythagoras theorem to show that the road from A to B is 50 miles long. I let x be the number of miles from A to D and y be the number of miles from C to D.
Since CD is perpendicular to AB, triangles ACD and DCB are right triangles. Write down Pythagoras theorem for each of these triangles. This gives you two equations in x and y. Solve these equations to find x and y.
Penny


