Name: AJ
Grade: 11th
Student

Question:
I have a question regarding Octagons. I have calculated the answer, but want to check my math, ran across your website and hope you can help me.

I am working a project for my shop class and need to know the square footage for an octagon with equal 10foot sides. Each wall will be exactly 10 feet long. This should equate to 478Sq. Ft., according to my calculations. I appreciate your help very much.

thanks,
aj

Hi AJ,

Imagine that you cut you octagon into 9 pieces as in the diagram.

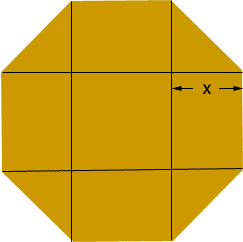
You get a 10 foot by 10 foot square in the middle, 4 rectangles and 4 isosceles, right angles triangles. The key is to find the length x in the diagram.

The square has area 100 square feet.

Each triangle has hypotenuse of length 10 feet and two other sides of length x feet. Thus, by Pythagoras theorem

x² + x² = 10² = 100

Thus

2 x² = 100 and hence
x = 5√2

Hence each rectangle has area 10 5 √2 square feet.

Each triangle has area ¹ /₂ 5 √2 5 √2 square feet

Thus the area is

100 + 4 (10 5 √2) + 4 ( ¹ /₂ 5 √2 5 √2) square feet.

I get 482.8 square feet.

Penny