Question: I know the base length of my arc (10 inches) - I also know the height at the center to the arc (2 inches). I don't think the end is at the midpoint tho. How do I figure out how long the arc length is?

My question involves being able to cut a round pipe into an arc that is 10 inches wide and 2 inches tall. I need to know the smallest diameter pipe to buy in order to fulfill these requirements.

Please help!?!

Thank you in advance.

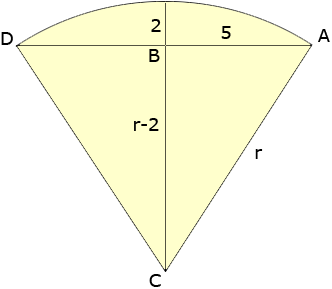
Hi,

I am not sure I understand your question but I assumed that you have a circular arc. Let us know if we haven't interpreted the question correctly.

I drew a diagram, labeled the radius r an drew a line from the centre C to the midpoint of the arc.

The triangle ABC is a right triangle so, by Pythagoras theorem,

5² + (r - 2)² = r², or
25 + r² - 4r + 4 = r², or
r = ²⁹/₄ = 7.25 inches.

Thus you need pipe with a diameter of 14.5 inches.

If you need to find the length of the arc then that involves some trigonometry.

cos(BCA) = ^{(r - 2)}/_r = ^5.25/_7.25 = 0.7241

and hence the measure of angle BCA is cos^-1(0.7241) = 0.7610 radians and thus the measure of angle DCA is 2 0.7610 = 1.522 radians.

The length a of the arc is given by

a = r angle(DCA) = 7.25 1.522 = 11.42 inches o almost 11.5 inches.

Penny