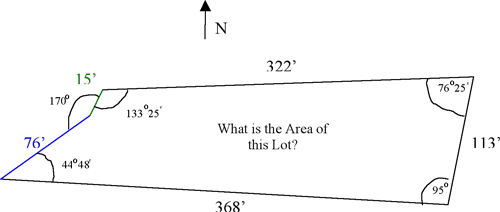
How do you calculate the area of the following Lot?

I figured the following angles from the deed, which read:

            N 86 degrees, 45 minutes E, for 322 feet.

            S 10 degrees, 30 minutes W for 113 feet.

            N 84 degrees, 30 minutes W for 368 feet.

            N 50 degrees, 42 minutes E for 76 feet.

            N 40 degrees, 40 minutes E for 15 feet.

There is a discrepancy between two surveyors and I’d like to figure out how to calculate the Area of such a shape. 

Other – I am not a student or teacher, just looking to buy a piece of land.

Thank you.

Ben

 

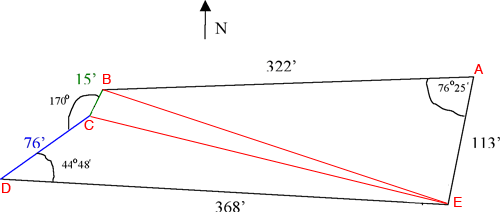
Hi Ben,

I reproduced the diagram you sent

I divided the lot into three triangles and labeled the vertices.

I am going to find the lengths of the two lines I added using the law of cosines, so I need to express the angle measurements using decimal fractions of degrees so that I can use my calculator to calculate the cosines.

25' is 25/60 = 0.417o and 48' is 48/60 = 0.8o

Thus the measure of angle A is 76.417o and the measure of angle D is 44.8o .

The law of cosines, applied to triangle ABE gives

|BE|2 = |AB2| + |EA|2 - 2|AB||EA| cos(A)
= 3222 + 1132 - 2 322 113 cos( 76.417o )
= 103684 + 12769 - 72772 0.23485
= 99362.225

Ant thus |BE| = √ 99362.225 = 315.21 feet.

In a similar fashion I found |EC| = 318.61 feet

Now I can use Heron's formula to calculate the areas of the three triangles.

For example, for triangle ABE let a = 113, b = 322 abd c = 315.21, then

s = (a + b + c)/2 = 375.105 and area = Sqrt[s (s - a)(s - b)(s - c)] = 17683.9 square feet.

Similarly the area of triangle BCE is 2314.31 square feet and the area of triangle CDE is 9854.33 square feet. Thus the area of your lot is

17683.9 + 2314.31 + 9854.33 = 29852.5 square feet.

There are 43560 square feet in an acre so your lot has an area of

 29852.5/43560 = 0.69 acres

Harley