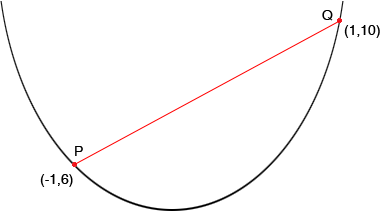
Verify that the function satisfies the hypotheses of the Mean Value Theorem on the given interval. Find all numbers "c" that satisfy the Mean Value Theorem. 11. f(x)=3x² + 2x +5 [-1, 1]

If you could help me understand what to do and why that would be great.

Hi Candace,

I expect that in your textbook the conditions given for the Mean Value Theorem are either that "f(x) is differentiable for all x in [a,b]" or that "f(x) is differentiable for all x in (a,b) and continuous for all a in [a,b]". The function f(x)=3x² + 2x +5 is differentiable for all values of x and hence it satisfies the conditions for any interval [a,b] and hence in particular for [-1,1].

f(1) = 3 1² + 2 1 + 5 = 10 and f(-1) = 3 (-1)² + 2 (-1) + 5 = 6. I drew a rough sketch of the graph of
f(x) = 3x² + 2x +5 and put the points P(-1,6) and Q(1,10) on the graph.

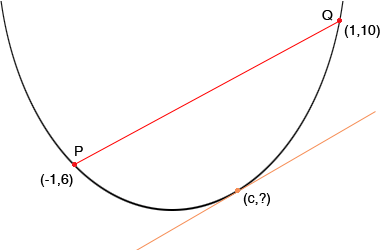
The conclusion of the Mean Value Theorem is that somewhere on the curve between P and Q there is a point where the tangent line is parallel to the line joining P and Q. The first coordinate of this point is the number "c" in your problem. Before I try to find c using calculus let me put it on the curve where I think it will be. I just tried to find a point where it looks like the tangent line is parallel to the line joining P and Q. I used ? for the second coordinate of this point since I don't care what it is, I just want to find c.

Algebraically I can tell if the two lines are parallel by calculating their slopes. I know the coordinates of P and Q so the slope of the line joining P and Q is

 ^{(10 - 6)}/_{(1 - (-1))}  = ⁴/₂ = 2

The second line is the tangent to the curve at the point (c,?) so its slope is f '(c). f '(x) = 6x + 2 and hence the slope of the tangent at (c,?) is f '(c) = 6c + 2. Thus the two lines are parallel if

6c + 2 = 2 that is 6x = 0 or c = 0.

Your textbook probably has the conclusion that

f '(c) = ^{(f(b) - f(a))}/_{(b - a)} 

But that is exactly what we did. f '(c) = 6c - 2 and  ^{(f(b) - f(a))}/_{(b - a)}  =  ^{(10 - 6)}/_{(1 - (-1))} =2

Penny