This is a trigonometry question?

A regular octagon is inscribed in a circle of radius 15.8 cm. What is the perimeter of the octagon?


My name is Carlin, if you could tell me where to begin on the answer it would be of help.

Thanks

 

Hi Carlin,

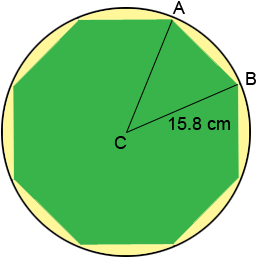
In the diagram above C is the centre of the circle. The octagon can be divided into 8 triangles congruent to ACB and hence the measure of the angle ACB is 360/8 = 45 degrees. Thus the triangle ACB is isosceles, with two sides of length 15.8 cm each and the angle between them measuring 45 degrees. Can you find the length of the third side?

Write back if you are still stuck.
Penny