The base of the pyramid is 100 blocks by 100 blocks; each successive layer is one less block wide and deep until the top layer which is simply one block. Each block is 97 cm wide by 97 cm deep by 63 cm tall. If one liter of paint can coat exactly three square meters how many liters are required to coat the entire exposed surface of the pyramid? Round up to the nearest liter.
The answer is 7252 but I can not get the right answer myself. How is it figured out?
Hi Cindi,
I'm going to start with a much smaller pyramid, one where the base is 3 blocks by 3 blocks.
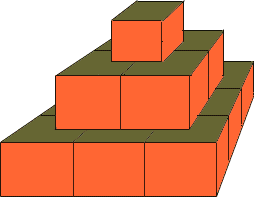
First I am going to paint the faces of the blocks, the orange part of the diagram. Each face is 63 cm by 97 cm. Around the base that gives an area of
63
97
3
4 square cm
Around the next row the area is
63
97
2
4 square cm
and around the top row the area is
63
97
2
4 square cm
Thus the total area of the faces is
63
97
3
4 + 63
97
2
4 + 63
97
2
4
= 63
97
4
(3 + 2 + 1)
= 63
97
4
6 square cm
Now paint the tops of the blocks. If you look down from the top you see

Which has an area of
(97
3)2 square cm
Thus the total area to be painted is
63
97
4
6 + (97
3)2 = 231345 square cm, or
231345/(100100) = 23.1345 square meters
Each liter of paint covers 3 square meters so you need 23.1345/3 = 7.71 liters hence 8 cans of paint.
For your problem the area of the faces is
63
97
4
(100 + 99 + 98 + ··· + 1) square meters
and for the area of the top is
(97
100)2 square cm
To evaluate the sun 100 + 99 + ... you may want to add from both ends to the middle.
Penny


