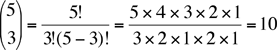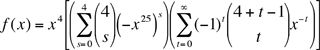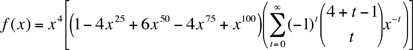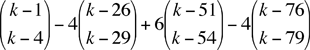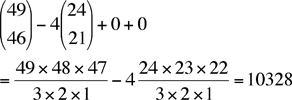|
 |
| Name: dan Who is asking: Student Level of the question: Secondary Question: Simply put, I am curious to find the likelyhood of each possibility (4-100) if I were to roll 4 25-sided die. It seems to start off simply, as 1, 4, 10, 20...following the inside diagonal of Pascal's triangle. But as soon as i reach the point where the sum is greater than the number of sides, Pascal's no longer seems to work. I would be greatly appreciated if I could be informed of the proper formula to find this answer, or perhaps if my theory of doing it is wrong. |
|
Hi Dan, On a roll each die will show a number between 1 and 25. Let k be the sum of the four numbers that appear on the dice, then 4 ≤ k ≤ 100. We solved this using generating functions, so for each k we need the we need the coefficient of xk in the polynomial
There is a common factor of x4 in this expression so
Next we expanded using the binomial theorem but first we should say something about notation. The symbol
So, for example Now, back to expanding using the binomial theorem. This is an infinite sum but, inside the square brackets we want the coefficient of xk-4 where 0 ≤ k-4 ≤ 96. We get the coefficient to be Here we have used the convention that
Thus, for example, if k = 50 then the coefficient of x50 is Andrei and Shawn |
 |
 |
 |
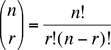 where , for any positive integer k, k! = k
where , for any positive integer k, k! = k