|
 |
| About y = 5x + 24 and y = -3x - 8 1. Graph both equations on the same set of axes. When you made your graph, how did you choose the range of x and y values? 2.Find the point of intersection for the graphs. 3. Test the point of intersection you found by substituting its coordinates into the equations. Do the coordinates fit the equations exactly? Thank for your teaching. |
|
I am going to change the problem by looking at the functions
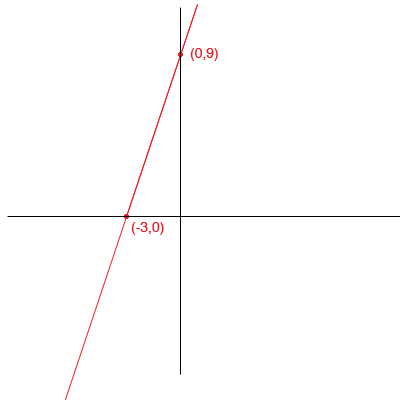
The first thing I would do is to use a piece of scrap paper and draw a rough sketch using the intercepts. For the first function
When x = 0, y = 9 so (0,9) is on the graph and when y = 0, x = -3 so (-3,0) is on the graph.
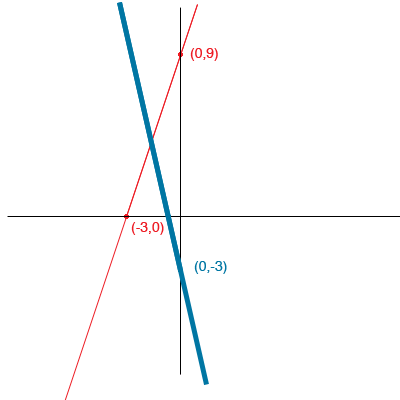
Now add the second function
When x = 0, y = -3 so (0,-3) is on the curve. When y = 0, x = -3/5
I purposefully didn't mark the x-intercept of the second line on the graph and drew the line thick because I am not trying to be accurate here, I am just trying to see what ranges I should choose for the x and y values when I draw an accurate graph. What I see here is that if I draw a graph with the x values between -4 and 1, and the y values between -1 and 10 then the point where the lines cross will be on my graph.
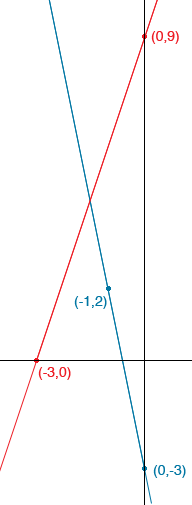
To graph the second line I substituted x = -1 and got y = 2 to find a second point on the graph. I used this point rather than the x-intercept so that I didn't have to use fractions. I also didn't mark a scale on the axes, but you will need to do this to answer part 3. The equations are
hence
Simplifying gives me
Substituting this value into the first equation I get y = 9/2 This looks approximately correct on my diagram, that is the curves intersect at x = -2/3, y = 9/2 Penny |
 |
 |
 |