Question: Hello there.
I've been trying to solve this problem for a few days now to to no avail, and I can't seem to fully understand what this problem requires. I would really appreciate any help that you would be able to give me regarding this.

The given problem is so:

A point moves so that its distance from the line y=5+2x is twice its distance from the line y=5-2x. Find the general form of the equation of its locus.

What I'm not sure about it what I'm actually solving for. Am I looking for the equation of a line, parabola, circle, ellipse, or hyperbola? I researched that a locus is a collection of points which share a common property--so most likely, you can graph it to form a type of figure. But I can't figure out what figure that it could be.
Also, I'm not sure about how the point moves about the two lines. Is the distance measured perpendicularly? Or is it possible for the point to move in any direction at all?

I have a graph and have begun solving for the distance from the point to each of the lines, but so far, I can't come up with a rational solution to the problem. This deals with analytical geometry, so I've pretty much exhausted most of my knowledge about this course on this problem.

Thank you so much for your time.

Sincerely,
Hazel

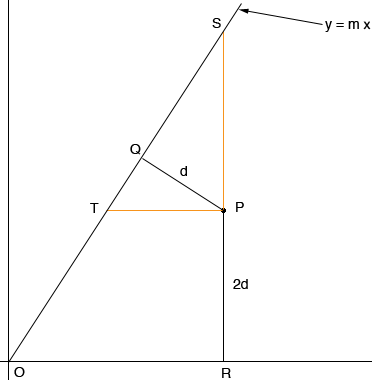
Hi Hazel,

You have two lines that intersect on the y axis at (0,5). My first approach is to imagine that I translate the diagram downwards 5 units so that the line intersect at the origin, and the rotate the diagram so that the line y = 5 + 2x lies along the x axis. This will not change the shape of the locus, so if I can fond the shape in this position then I will know the shape in the original position.

In the new position the line y = 5 - 2x become a line y = mx. I chose a point that satisfies the required property and called it P. I let d be the distance from P to the line y = mx. Below is my diagram.

Angle PQT is a right angle so angle QTP plus angle TPQ is 90 degrees. Also angle TPQ plus angle QPS is 90 degrees so angle QTP is congruent to angle QPS. Also angle PSQ is congruent to angle TPQ so triangles QTP and SQP are similar. Thus

  ^|SP|/_|TP| = ^|SQ|/_|QP|   

But t ^|SP|/_|TP| is m, the slope of the line so

|SQ| = m d

The important fact here is that |SQ| is a constant times d.

Now apply Pythagoras Theorem to triangle SQP and you will see that |SP| is also a constant times d. Hence |SR| is a constant times d. But |SR| is the y-coordinate of S, and the y-coordinate of S satisfies = y mx. Thus the x-coordinate is a constant times d. But the x-coordinate of P is the same as the x-coordinate of S and thus the coordinates of P are

(a constant d, 2 d)

Hence the y-coordinate of P divided by the x-coordinate of P is a constant. If you do this carefully you will see that this constant only depends on m. I want to call this constant k.

Hence every point on the locus satisfies y = k x. Hence the locus is a line through the origin. Now move the diagram back to the original position and the required locus is a line through the intersection point of the two given lines.

Actually I biased the argument by placing P below the line y = mx. If P is above the line y = mx you get another line and hence the locus is two lines that intersect at the point of intersection of the two given lines.

Penny