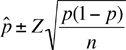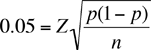I have to do a research about the behavior of library users. We are going to apply a survey to a population of 1280 students (Management an Economics students) but of course we have to do it to a sample....I need to know the size of my sample.

Well, the information I know is that

d= precision...and in this case d= 0.05

q= 1-p

p= is the "expected ratio" (proportion esperada, in spanish)....I am not sure if this is 0.03 or 0.05

Z= is the Confidence Intervals. We use the 95% so Z= 1,96

I tried to use the formula...but I can't get a result. I haven't found a book with this formula so that I could see some examples.

I don't know what other kind of information you need. I will be thankful if you can help me

Ivonne

 

Hi Ivonne,

The confidence interval expression for the proportion in a binomial distribution is

You want the precision to be 0.05 and hence you want your confidence interval to be

Hence

It is this expression that gives you the sample size. You know Z and you have an estimate for p (0.03 or 0.05) and hence you can find n. Squaring both sides and solving for n gives

n = ( Z/0.05)2 p(1 - p)

You are asked for a 95% confidence interval so Z = 1.96 and hence if the expected ratio is 0.03 then

n = ( 1.96/0.05)2 0.03(1 - 0.03) = 44.7

With sample size estimates you must round up so I get a sample size of 45.

Penny