Julie
Grade 12
Parent of Student

A car travels west at 24 km/h. at the instant it passes a tree, a horse and buggy heading north at 7 km/h is 25 km south of the tree. Calculate the positions of the vessels when there is a minimum distance between them.

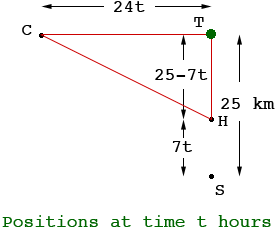
Hi Julie,

In your mind you should see this as a moving picture. The car is moving west, away from the tree, and the horse is moving north, towards the tree. The best I can do is to draw a diagram that shows the situation at one instance of time, a snapshot at time t hours.

In my diagram T is the tree, C is the car, H is the horse and S is the position of the horse at time t = 0, this is the instant when the car passed the tree. The distance from S to T is 25 km.

The car is travelling at 24 km/h and hence in the t hours before I took the snapshot the car had travelled 24t km. In this time the horse travelled 7t km so the distance from the horse to the tree is 25 - 7t km.

I then drew a red, right triangle on the diagram and the length |CH| is the distance from the car to the horse. Use Pythagoras Theorem to express |CH| as a function of time t, and then use calculus to find the time when |CH| is a minimum.

Penny