Hi there, I am an art student and in the process of making a cone out of sheet metal. I am unable to work out the template I need to produce my final cone. The dimensions I have are that the final cone will be 58mm high and will have a diameter of 102mm. Can you help?

Thanks, Laura

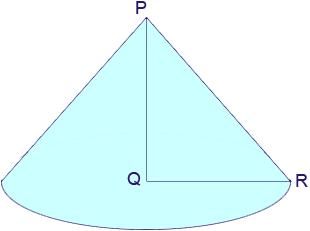
Hi Laura,

I drew a picture of your cone and labeled some points.

|PQ| = 58 mm and |QR| = 51 mm and the triangle PQR is a right triangle so be Pythagoras Theorem

|PR|² = |PQ|² + ||QR|² = 58² + 51² = 3364 + 2601 = 5965

so

|PR| = √5965 = 77.23 mm.

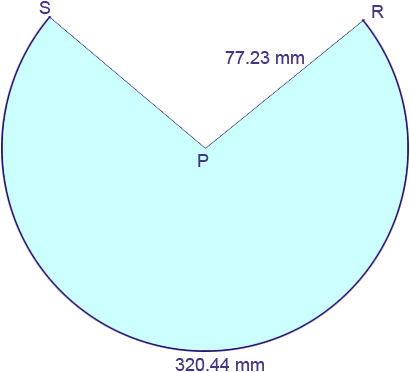
Thus when you cone is rolled out flat it is a sector of a circle of radius 77.23 mm.

The length of the arc RS is the circumference of the circle at the base of your cone. This is a circle of radius 51 mm and the circumference of a circle of radius r is given by

circumference = 2 r = 2 51 = 320.44 mm.

All that remains is to determine the measure of the angle RPS. The relationship between the length of the arc of a sector of a circle, the radius of the circle and the angle at the center is

arc length = radius angle

where the angle is measured in radians. Thus

320.44 = 77.23 angle

so

angle = ^320.44/_77.23 = 4.15 radians.

There are radians in 180^o and hence 4.15 radians is

4.15 ¹⁸⁰/ = 237.7^o

Hence you need to draw a circle of radius 77.23 mm, cut out a sector with centre angle 360^o - 237.7^o = 122.3^o . What remains is your template.

Penny