|
Linden,
I would start by sketching a diagram.
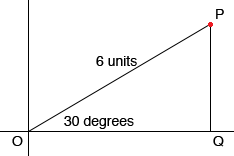
In my diagram O is the pole, which will be the origin in the Cartesian system, and P is the point with polar coordinates (r,theta) = (6,30o). I drew a perpendicular line from P to Q on the polar line, which will be the X-axis in the Cartesian system. I now have a right triangle POQ where the length of OQ is the X-coordinate of P and the length of PQ is the Y-coordinate of P. I can find these lengths in two ways.
First method:
I know that any triangle with angles 30, 60 and 90 degrees has side lengths in the ratio if 1 to 2 to √3. (These triangles come up so often that this is a fact I remember.) 2 is the length of the hypotenuse, 1 is the length of the shorter leg and √3 is the length of the longer leg. In the triangle above the length of the hypotenuse is 6 units so the length of the shorter leg, |PQ| is half of that which is 3 units. The length of the longer leg is √3 times the length of the shorter leg so |OQ| = √3 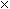 3. Thus P has Cartesian coordinates (3√3, 3). 3. Thus P has Cartesian coordinates (3√3, 3).
Second Method:
Use trig functions.
sin(30o) = |PQ|/|OP| = |PQ|/6 = 1/2 and therefore |PQ| = 3.
cos(30o) = |OQ|/|OP| = |OQ|/6 = √3/2 and therefore |PQ| = 3 √3.
Thus P has cartesian coordinates (3 √3, 3)
Penny
|





