Name: Lindsey
Who is asking: Student
Level of the question: Secondary
Question: I need to find the quadratic equation in the form:
f(x)=a(x2 - (-b/a)x + (c/a))
The vertex is (1, -7), the roots are (4, ?)
I need to find the other root but I don't know where to begin. My answer key says the other root is (-2). How is this possible?
Hi Lindsey,
I expended the equation to put it back into the generic form
f(x) = a x2 + b x + c
I can show you two ways to solve this problem. One solution is geometric and is the method I prefer so I am going to do it first.
This quadratic equation is the equation of a parabola that either opens upward if a > 0 or downwards if a < 0. In either case it is symmetric about the vertical line through the vertex. In your example this is the line x = 1. To the right of x = 1, the graph crosses the x-axis at x = 4.
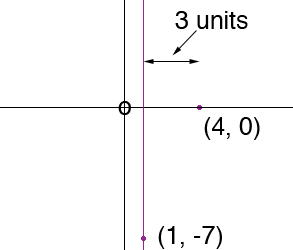
Thus the graph crosses the x-axis 3 units to the right of the line of symmetry. By the symmetry the graph must cross the x-axis 3 units to the left of the line of symmetry, that is at x = -2.
The second method of solution is algebraic. To use this method you need to know that the vertex of the parabola
f(x) = a x2 + b x + c
occurs at x = -b/2a
Since the vertex is at (1, -7) this gives
1 = -b/2a or b = -2 a (equation 1)
The y-coordinate of the vertex is -7 so
a 1 2 + b 1 + c = -7 or a + b + c = -7 (equation 2)
Finally there is a root at x = 4 so
42
a + 4
b + c = 0 that is
16 a + 4 b + c = 0 (equation 3)
Solve equations 1, 2 and 3 for a, b and c.
Penny


