Manish,

If you had the hat and cut it straight up from the base to the peak

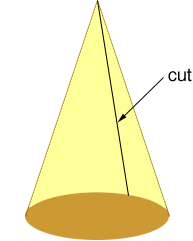
and rolled it out flat you would have a sector of a circle.

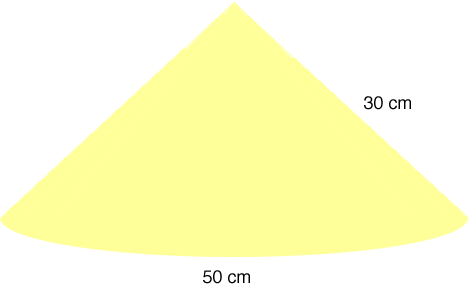
The relationship between the radius r, the length of the arc a and the angle at the center theta is

a = r theta

where the angle is measured in radians. You have a = 50 centimeters and r = 30 centimeters. Hence

50 = 30 theta, and hence
theta = ⁵⁰/₃₀ = 1.67 radians.

which is

1.67  ¹⁸⁰/ = 95.7 degrees

My suggestion is that you make a paper model of the hat before you make the real one. I would make the centre angle a little larger than 95.7 degrees so that you have some overlap when you roll it into a cone.

Penny

We received a reply,

The reply is absolutely fantastic, however, the height that I mentioned in the query was the vertical height(30 cms) and not the slant height,would that change things?

Oops, I misread your question. To answer your question correctly I need to draw a triangle ABC inside the cone with A at the apex of the cone and B at the centre of the base.

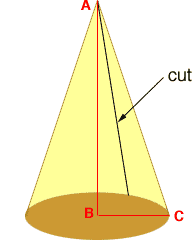
The length of AB is 30 cm and the length of BC is the radius of the circle. The circumference of the circle is 50 cm and the relationship between the circumference and the radius is

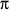
circumference = 2 radius

Thus

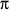
50 = 2 radius

and hence the radius is ⁵⁰ /₂ = 7.96 cm.

The triangle ABC is a right triangle so by Pythagoras Theorem

|AC|² = |AB|² + |BC|²

Thus

|AC|² = 30² + 7.96²

and hence the slant height |AC| is 30.1 cm.

Now I can go back to the second diagram in my first answer and change the slant height to 31.0 cm and continue as before

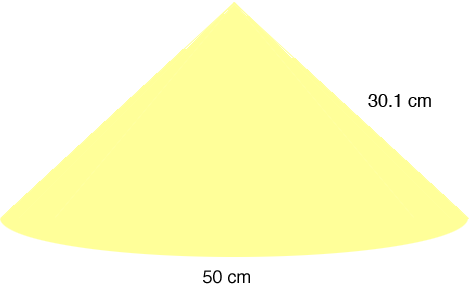
The relationship between the radius r, the length of the arc a and the angle at the center theta is

a = r theta

where the angle is measured in radians. You have a = 50 centimeters and r = 30.1 centimeters. Hence

50 = 30.1 theta, and hence
theta = ⁵⁰/_30.1 = 1.66 radians.

which is

1.66  ¹⁸⁰/ = 95.1 degrees

Penny