Question: I need to make a large cone segment. The large end has ID of 57 inches and the small end has ID of 23 inches. The cone is essentially a 45 degree cone (90 degrees at the tip). The sides of the segment are 2 feet long. How do I lay out a flat pattern that will fold into this segment? I need to know radius 1 and radius 2 and the angle the piece must be.

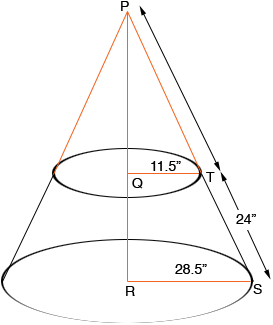
Nick,

I drew a diagram of and labeled some points.

The "flat pattern" will be part of a circle of radius |PS| so I need that length. I know that |TS| = 24" so I need to find |PT|. The triangles PQT and PRS are similar so 

 ^|PS|/_28.5 = ^|PT|/_11.5 or  ^{(|PT|+ |TS|)}/_28.5 = ^|PT|/_11.5

and hence

^{(|PT|+ 24)}/_28.5 = ^|PT|/_11.5

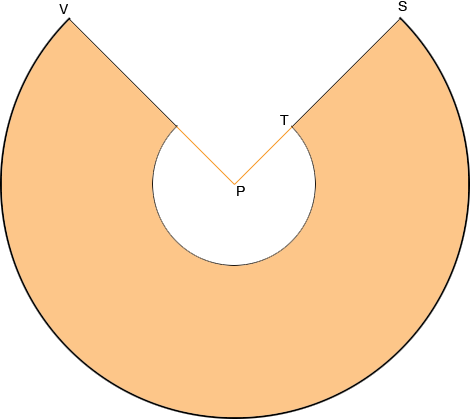
I solved for |PT| and got |PT| = 16.24", and thus |PS| = 24 + 14.24 = 40.24".

I can now see that the "flat pattern" is part of a sector of a circle of radius 40.24".

All that remains is to determine the measure of the angle SPV.

The relationship I need to use here is

a = r theta

where a is the length of the arc SV, r is the radius |PS| and theta is the measure of the angle SPV in radians. The length of the arc SV is the circumference of the base of the cone. The base of the cone is a circle of radius 57" so

a = 2 radius = 2 28.5" = 179.07 "

Thus

a = r theta gives 179.07 = 40.24 theta

This gives theta = 4.45 radians. There are radians in 180^o so 4.45 radians is

  ¹⁸⁰/  4.45 = 254.0^o

Draw two concentric circles of radius 40.24" and 16.24". Remove a sector with centre angle of 360⁰ -254^o = 106^o and roll up what remains to form the truncated cone.

Penny