Question: I am having trouble with making it simple to the students how to do the probability of "Z" when it is a normal variable. Can you show me steps to make it simple?

Problem: Find the probability of Z when it lies between -1.10 and -0.36
Thanks

Hi Pat,

You should imagine that you have a population where the measurement of interest has a standard normal distribution. Perhaps you have a machine that produces some widgets and you have measured the lengths X of these widgets for years and you know these lengths have a normal distribution with some mean mu and variance sigma. If you calculate

Z = ^{(X - mu)} /_sigma

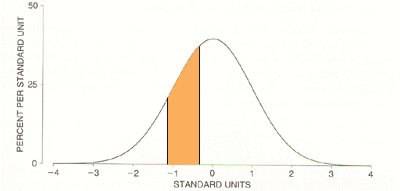
Then Z has a standard normal distribution.

You are concerned that the machine is out of calibration so you select a newly produced widget at random and for this widget measure Z. What is the probability that the Z value you get is between -1.10 and -0.36?

I think of this probability as an area. Below is a graph of the standard normal distribution and I have shaded the region under the curve between -1.10 and -0.36. The probability that the Z value you get is between -1.10 and -0.36 os the area of the shaded region.

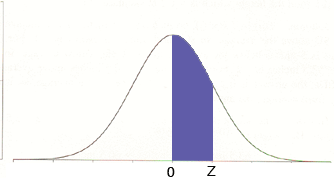
This probability you can compute using the standard normal distribution in your textbook. The layout of the table depends on the book you are using but I expect that it has a graphic at the top of the table that looks like

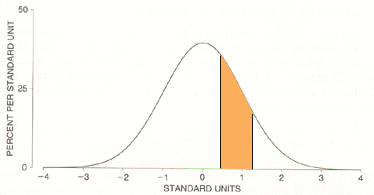
and the values in the table give you the area under the curve between o and Z, that is the region shaded blue in the diagram.

To find the probability that you want the first thing to notice is that because of the symmetry of the diagram. the area under the curve between -1.10 and -0.36 is the same as the area under the curve between 0.36 and 1.10.

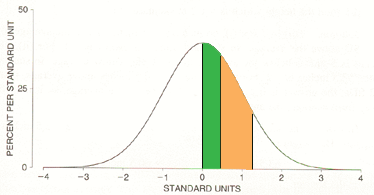
From the table I have I found that the area under the standard normal curve between 0 and 1.10 is 0.3643.

Finally to find the area (probability) you want I need to subtract the area under the curve between 0 and 0.36, the area shaded green in the diagram below.

In my table I found this area to be 0.1406. Thus the probability that Z is between -1.10 and -0.36 is

0.3643 - 0.1406 = 0.2237

Penny