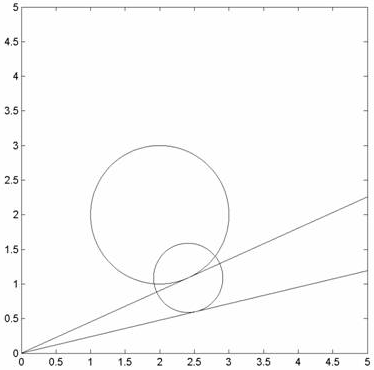
My name is Paul and I'm a student with the following question. I think
the level of the question is approximately high school but not totally
sure.

Question
============

Consider a circle whose center is (2,2) and whose radius is 1, and the
straight line that goes through the origin and that is tangent to this
circle so that the intersection between them is as shown in the attached
picture. With this new point we make a new circle whose radius is half
of the first one, and we calculate the corresponding intersection point
with the same suppositions as in the first case. We repeat the process
to the infinite. Find the distance between the center of the circle in
the infinite and the origin (point (0,0)).

This is what I have so far ,

Equation of circle
--> (x-2)² + (y-2)² = 1

If the first point of tangency is (a,b) then a second equation is
--> a² + b² = 8 - 1²

This where I'm stuck and need some help to solve the problem.

Thanks,

Paul,

The circles are not really relevant -- you just need the fact that a radius is perpendicular to the tangent at its point of contact. You get a sequence of right triangles, so use the Pythagorean theorem to get what is called a geometric series, namely 8 - (1 - 1/4 - 1/16 - 1/64 - ...). The terms you subtract look like 1/(4^k).

Chris