Name: Rahul
Who is asking: Student

Question: Hi,
I am Rahul. I am in Year 10 and Planning to do GCSE early.
My question is:
I have problem in finding area of polygons. I don't know the formula to find area of pentagon, hexagon and so on. Can you help me.

 

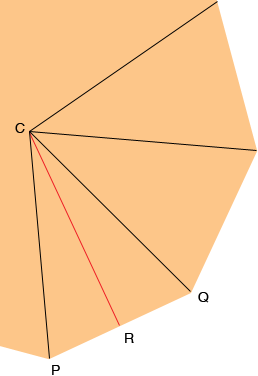
Rahul,

I am going to assume that you are considering regular polygons. That is a polygon which has all it sides of the same length and all the interior angles congruent. I am also going to assume that you know the side length s, and the number of sides n. Here is a piece of one such polygon.

C is the centre of the polygon, that is the point that is equidistant from each of the vertices. Join each vertex to C to partition the polygon into n congruent triangles. CPQ is one such triangle and hence

the polygon area is n times the area of triangle CPQ.

Since these triangles are congruent

the measure of the angle QCP is 360o/n 

Let R be the midpoint of PQ then CRQ is a right angle and the measure of angle QCR is  360o/2n and the length of RQ is s/2 . Hence

 |RQ|/|CR|  = tan(  360o/2n )

Since |RQ| =  s/2 you can find |CR| and the area of the triangle CPQ is 1/2 s |CR|.

Penny