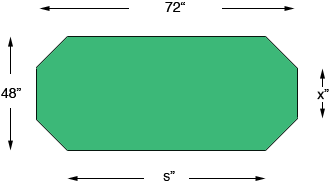
Question: I am building a poker table which is in the shape of an irregular octagon. I know the table measures 72 inches long and 48 inches wide with two parallel straight sides of equal length and six smaller sides of equal length ( three at each end of the table), what I don't know are the lengths of the any of the sides.

Robert,

Her is what I understand as your table top.

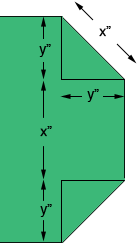
I let the long side length by s inches and each of the six short side lengths be x inches.

Here is a closer look at one of the ends.

The triangle shown is a right triangle and hence, by Pythagoras Theorem,

y² + y² = x² or 2 y² = x² and hence y = ^x/_√2

Thus the width of the table, 48 inches, can be written

48 = y + x + y = ^x/_√2 + x + ^x/_√2 = (1 + ²/_√2 ) x = (1 + √2) x

Hence

x = ⁴⁸/_{(1 + √2)} = 19.88" or 19 ⁷/₈ inches

Thus the length of the long side is

s = 72 - 2 (19 ⁷/₈ ) = 32 ¹/₄ inches.

Harley