Question: These two questions from my math textbook I have been working and they still confuse me and i have no idea how to solve them...o_O...thanx 4 your help in advance :).

#1. A manufacturer determines that the cost of producing x of an item is C(x)=0.015x²+12x+1000 and the price function is p(x)=250+2x/10. Find the actual and marginal profits when 500 items are produced.

#2. At 9 a.m a car is 10km directly east of Marytown and is traveling north at 100 km/h. At the same time, a truck leaves Marytown traveling east at 70 km/h. At 10 a.m, how is the distance between the car and the truck changing?

Shimaera,

Profit, P(x), is revenue minus cost and revenue is the price you charge per item, time the number of items you sell, thus

P(x) = revenue - cost
= p(x) x - C(x)
= x ( 250+2x/10) - (0.015x²+12x+1000)

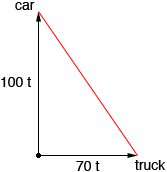
Simplify this expression and then the profit when 500 items are produced is P(500).

The marginal profit is the additinal profit obtained by producing one more item. This is approximated by the derivative of the profit with rrespect to the number of items produced. Hence find the derivative of P(x) and evaluate it at x = 500.

For question 2 let t be the time after 9 am in hours. Since the car is traveling 100 km every hour, after t hours it has progressed 100 t km north of Marytown. The truck has traveled 70 t km east of Marytown.

Use Pythagoras Theorem to find the distance between the car and the truck (the length of the red line segment in the diagram) and then differentiate this expression to find the rate at which the distance between them is changing.

Penny