Travis
Secondary (10-12)
College Student


I am looking to do a project for work where I must find the radius of an octagon but I cannot directly measure it. I’ve found that on a regular hexagon I can find the radius by using the distance between the bolts to find the radius to the line connecting the bolts but also to the outside of a circle to cut it out. I do not understand however how this works for an octagon. What do I do to find the radius of an octagon with only the ability to measure the distance of the bolts? The center has a cutout in it and is mounted currently and I cannot get accurate measurements.

Thank you for your help,
Travis

 

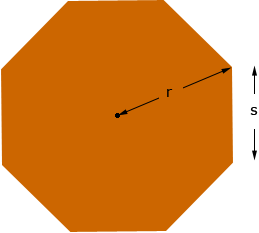
Travis,

I am not sure I understand but let me try. My understanding is that you have an octagon as in the diagram below, you can measure the distance s and you want to calculate the distance r.

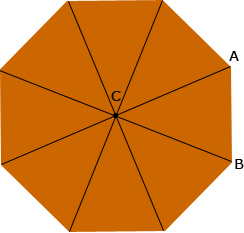
If my understanding of the problem is correct then you can proceed as follows.

If you join each vertex to the center C of the octagon then you divide the octagon into 8 congruent triangles.

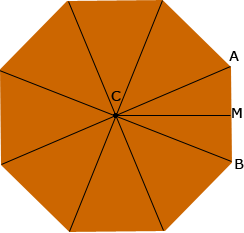
The measure of the angle ACB is then 130/8 = 45o. Draw a line from C to the midpoint M of the line segment BA then ACM is a right triangle, the length of AM is s/2 and the measure of angle ACM is 45/2 = 22.5o.

Using trigonometry sin(ACM) = |AM|/|AC|. But sin(ACM) = sin(22.5o) = 0.3827 and
|AC| = r, thus

r = |AM|/0.3827 = s/(2 * 0.3827) = s/0.7654 = 1.307 s.

Penny