Name: Wael
Level: first secondary
Who is asking: student
How is the area of an arc (alpha*pi*r squared/360) derived?
How is the length of an arc (alpha*pi*r/180) derived?

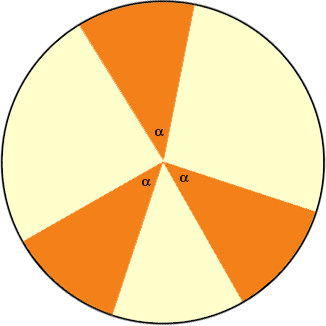
Wael,

The important factor that influences both of these expressions is the symmetry of the circle. If the central angle of a sector of a circle is alpha then the area of the sector is the same as the area of any other sector with central angle alpha, regardless of where the sector sits in the circle.

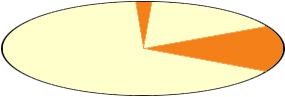
The same is not true for other plane figures. For example in an ellipse two sectors with the same central angle can have quite different areas.

The area of a circle of radius r is r². If you have a sector with central angle 180^o (half of 360^o) then the area of the sector is half the area of the circle. That is

 a sector with central angle 180^o has area ¹⁸⁰/₃₆₀ r² = ¹/₂ r²

If you have a sector with central angle 90^o (one-quarter of 360^o) then the area of the sector is one-quarter the area of the circle. That is

 a sector with central angle 90^o has area ⁹⁰/₃₆₀ r² = ¹/₄ r²

If you have a sector with central angle 36^o (one-tenth of 360^o) then the area of the sector is one-tenth the area of the circle. That is

 a sector with central angle 36^o has area ³⁶/₃₆₀ r² = ¹/₁₀ r²

The point I am making here is that the measure of the central angle is a fraction of 360^o and the area of a sector is a fraction of the area of a circle, and these fractions are the same. So one more example, if the measure of the central angle is ^o
( /₃₆₀ of 360^o) then the area of the sector is /₃₆₀ r²

A similar arguent is valid for the length of an arc. The measure of the central angle is a fraction of 360^o and the length of an arc is a fraction of the circumference of the circle, and these fractions are the same.

I hope this helps,
Penny