Hi Wendy,

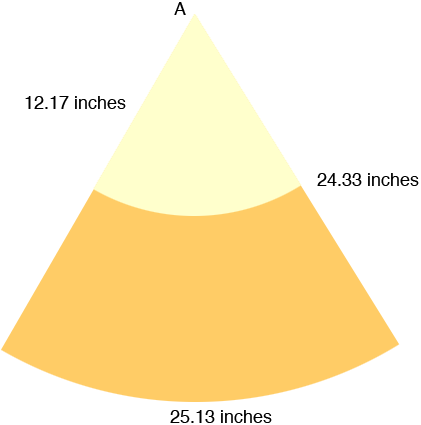
I drew a diagram of your truncated cone and then extended it to the vertex of the cone. x is the distance in inches from the top of your truncated cone to the vertex.

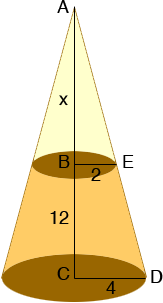
Triangles ABE and ACD are similar and the length of the base of ABE is half the length of the the base of ACD. Thus the height of ABE must be half the height of ACD. Thus x must be 12 inches.

I need the length of AD and I can find it using Pythagoras Theorem since ACD is a right triangle.

|AD|² = |AC|² + |CD|²
|AD|² = 24² + 4² so |AD| = 24.33 inches

Using the fact that triangles ABE and ACD are similar, |AE| is one half of |AD| so |AE| = 12.17 inches.

Now slice the cone from bottom to top and roll it out flat.

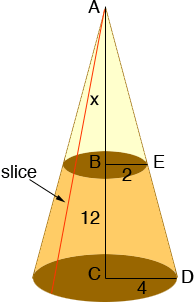
What you get is a sector of a circle of radius 24.33 inches. The length of the arc is the circumference of the base circle of the cone. This is a circle of radius 4 inches so the length of the arc is

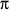
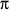
arc length = circle circumference = 2 radius = 2 4 = 25.13 inches.

The relationship among the length of an arc, the radius of the circle and the angle at the centre of the circle is

arc length = radius angle

where the angle is measured in radians. Thus

25.13 = 24.33 angle

and hence the angle is 1.033 radians. There are radians in 180^o and thus

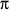
1.03 radians = ¹⁸⁰/ 1.033 = 59.18^o

Thus you need to draw a circle of radius 24.33 inches. Cut out a sector with a centre angle of 59.18^o . Cut out a sector of radius 12.17 inches and roll up what's left to form your slump cone.

I would try it out of paper first.

Penny