Hi Andy.

Unfortunately, it isn't nearly as simple as that. The short answer to your question is that 85% corresponds to about 7'11".

Now the long explanation:

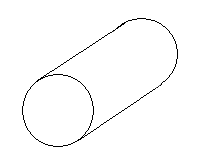I'm assuming that the cylinder is horizontal (that is, 10 feet high by 35 feet long).

When the substance in the tank is near the mid-fill level, each inch of depth corresponds to a much larger volume that when the substance is near the top or bottom of the tank. This means that to bring an empty tank up to 1" filled requires very little liquid, but to bring it from 5'0" to 5'1" requires quite a lot of liquid.

One thing that simplifies the problem is that the length doesn't matter. 85% of a long cylinder would be the same height as 85% of a shortened cylinder. This means that the length dimension doesn't even matter and we can simply think about the circular end.

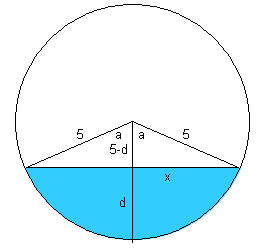So let's say the depth in feet is d. Let's draw some radii (5 feet each) and label the angle a as well. The line that is x units long is also labelled.

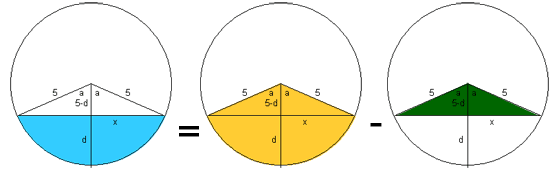
You can see from this diagram that one way to find the area in blue is to take the area of the sector and subtract the area of the triangular region.

The area of a sector is given by A_s = ½r² where is the included angle measured in radians. In our problem then,

But we need to calculate the angle a. We can do this by using the basic trigonometry function cosine. The right triangle inside has a hypotenuse of 5 and a side of 5-d, so cos a = (5-d)/5, therefore

Thus,

Now the area of the green triangle is just twice the area of the right triangle, which is ½ the base times the height, so the green triangle is base times height which makes

A_t = x(5-d)

But the value x isn't known yet. Since this is a right triangle, though, we can use Pythagoras to solve for x:

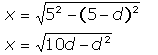
So

Now we can calculate the area of the blue region:

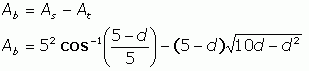
However, we are interested in the percentage of the area of the full circle (representing a full cylinder), not the actual area of the blue region. If we call the percentage P and the area of the circle A_c , then:

which we can re-arrange to solve for P, the percentage:

We know A_b , but need the value of the area of the circle:

Putting this in for A_c :

and substituting our expression for A_b :

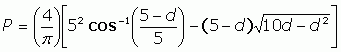
That's our final expression, which only depends on d (the depth). So if you measure the depth in feet and use that as d in this expression, you get the percentage of the cylinder that is filled. Remember to set your calculator for radians (not degrees) when using this equation or you'll get nonsense answers.

In particular, 7'11" is about 7.92' and

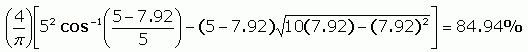
I graphed it using a spreadsheet package and found this relationship between the depth (horizontal axis) and percentage full (vertical axis):

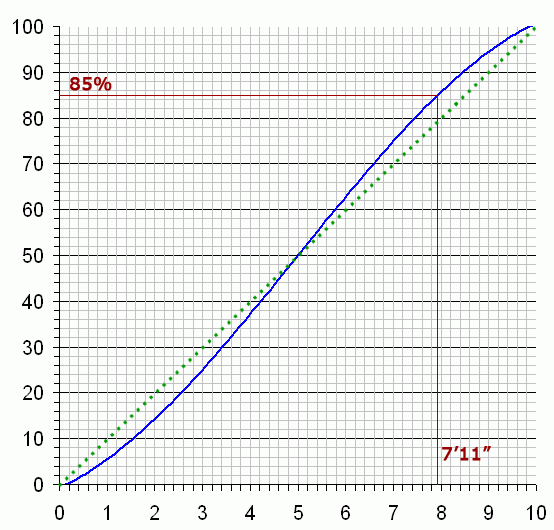
The dotted green line shows you how far off you would be if you just used a linear (85% of volume = 8.5 feet) method of calculation.

Hope this explanation is helpful,
Stephen La Rocque.